El famoso dinero de Bill Gates, II (cuestión de matemáticas)

Iba a editar la entrada anterior, pero mejor creo una nueva, que creo que queda más claro.

Es que se me había olvidado comentar una cosa importante (bueno, lo comenté, pero muy sucintamente): LAS MATEMÁTICAS, nuestras amigas.

En la versión en castellano que publiqué el otro día, la redacción del reparto de premios era un poco confusa, así que aprovecho la coyuntura para poner una imagen que acompaña una de las versiones inglesas, y mostraros además otro caso de "no por tener logos, las cosas son reales".

De que esto era todo mentira espero que no os queden ya dudas, pero vamos a darle una vuelta de tuerca al reparto de dineros que presume:

- Por cada persona a la que se lo envíe, me dan $245
- Por cada persona que, habiéndolo recibido de mí, lo reenvíe, me dan $243
- Por cada persona que, habiéndolo recibido de alguien que lo recibió de mi, lo reenvíe me dan $241.


Bien, hagamos un supuesto: supongamos que fuese verdad.

Por cada vez que "alguien" envía el correo, Microsoft pagaría $245 al que lo está enviando, $243 al que se lo había enviado a él anteriormente, y $241 al anterior. En total, $729 por cada envío.

Lo que es muy difícil estimar es la cantidad de envíos que se pueden producir o haber producido a lo largo y ancho del planeta. He buscado en Internet, y le he preguntado a mi hermana matemática, pero no he podido dar con nada más concreto que "es una burrada imposible de calcular". Pero yo soy muy cabezota y voy a intentarlo.

La experiencia me hace estimar así a groso modo, que cuando la gente reenvía cosas lo suele hacer a unas 1o o 15 personas (cuando recibo cadenas con las direcciones a la vista, suele ser este número aproximadamente el que se ve en cada reenvío). Pongamos una media de 12, y que sepáis que creo que es una estimacion a la baja (y un inciso reflexivo: si yo recibo este correo y me lo creo, lo enviaría a por lo menos 1000 direcciones, por supuesto, faltaría más. Ya me apañaría para conseguirlas).

También a groso modo, y basándome en los emails reenviados que yo recibo, que de media tienen unos 10 o 15 destinatarios por reenvío, pero incluso teniendo 3 o 4 perduran, me atrevo a deducir que al menos 1 de cada 5 personas que reciben un reenvío, lo reenvían. Siguiendo con mi estimación a la baja, pongamos pues que esa es la proporción de reenvíos, 1 de cada 5.

Y por último, y basándome también en lo que veo en las cadenas que yo recibo, pongamos que se reenvía una sóla vez al día. Es decir, que si yo lo envío hoy, la gente que lo recibe no lo vuelve a enviar hasta mañana, y así sucesivamente. Es, una vez más, una estimación muy a la baja, y aún así veréis que resultado.

Bien. Ignoremos por simplicidad todos los envíos que se hayan producido hasta hoy; que seguro que ya habrían arruinado a Bill Gates, pero ignorémoslos. Supongamos que yo lo recibí del limbo y soy la primera en enviarlo.

Yo se lo envío a 12 personas. De esas 12 personas, 12/5=2.4 lo reenvían, cada una a otras 12, es decir a un total de 2.4x12=28.8. De esas 28.8, se producirán 18,8/5*12=69,2 reenvíos... y así sucesivamente. Se trata de una progresión geométrica de razón 12/5=2.4.

Ahora, la fortuna de Bill Gates está estimada en unos 47.000 millones de dólares. A razón de $729 el reenvío, tiene para pagar por 64.471.879 reenvíos. Con la progresión de difusión definida, ¿cuántos días duraría?

Sabemos que la suma de los n primeros números de una progresión geométrica de razón r es:


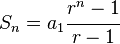
Sustituyendo Sn por 64.471.879, a1 por 1, y r por 2.4, podemos despejar el valor de n. Os ahorro los cálculos, pero el resultado final es 21: la fortuna de Bill Gates duraría 21 días a este ritmo de gasto. ¿Lo veis factible?


NOTA: si hay algún matemático en la sala, se agradecerá cualquier corrección.